Fluid dynamic instabilities and generation of turbulence
My research interests, which are within the general area of fluid mechanics (classical and non-classical) and applied mathematics, encompass theoretical, numerical and experimental aspects of transition from laminar to turbulent flows, turbulence, optimal and robust control applied to fluid mechanics, premixed laminar combustion, optimization techniques, possible chaotic behaviors in flight mechanics and mathematical biology.
Feel free to surf through the various sections of this page, which I tried to write in a form that should be understandable independently of your education level. If you end up finding something that interests you, please do not hesitate to contact me. This is particularly directed to students for possible research topics and researchers for possible joint works/collaborations.
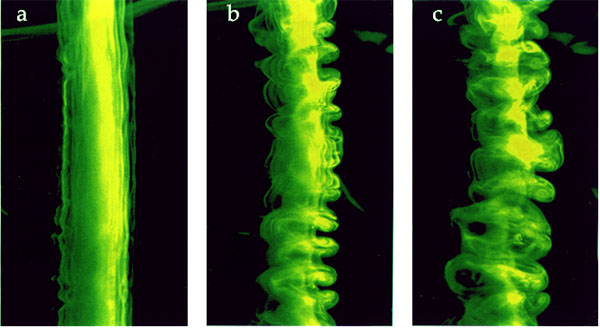
The majority of the research works here described are centered on flow stability and transition to turbulence. To have an idea of what this is, look at the picture above. It shows a flow visualization, that is a way to make visible to our eyes what happens inside the fluid. If you are curious enough, you might wander how this fluid undergoes different stages from a "regular" motion to "complicated" eddies. The answer is we do not know exactly. Hence, my interest in fluid dynamic instabilities and transition to turbulence.
Other fields of research, still within classical fluid mechanics, are chaos theory applied to airplane spin motion, stability of thin liquid films, flow control and optimization techniques. More recently I got involved also in the study of the Madelung fluid and in the numerical solution of the nonlinear Schrödinger equation of cubic type, which naturally arises from the stochastic quantization of a dilute system of N identical interacting Bose particles. As a consequence of my teaching duties, I have also approached the study of population dynamics and the interesting problem of spatial segregation in strongly-competing reaction-diffusion systems.
TopVortex reconnections, stemming from randomized velocity fields, play a pivotal role in the energy cascade, contribute to intricate mixing at small scales, and augment diffusion effects. These interactions also serve as the primary mechanism behind the generation of jet noise. If we interpret the axes of tubular vortex structures as turbulence's underlying framework, the entanglement of these axes signifies the topology of turbulence. Crucially, vortex reconnections alter this topology. This conceptual framework transforms into tangible reality when we shift from conventional viscous fluids to quantum fluids like superfluid liquid helium and atomic Bose-Einstein condensates.
In these quantum systems, rotational motion is confined to vortex lines with fixed circulation due to the constraints of quantum mechanics. Reconnections of individual quantum vortex lines manifest as discrete, striking events, which have been observed in both experimental and numerical settings. These events are fundamental for comprehending quantum turbulence, a disorderly state of vortex lines induced by stirring liquid helium and atomic condensates. In contrast, reconnections in classical viscous fluids are not complete occurrences; classical vorticity is continuous, leading to segments of initial vortical tubes being left behind as vortex threads. These threads then undergo successive reconnections in a cascade and mixing sequence as newly formed vortex connections recoil due to self-advection. Additionally, classical reconnections entail dissipative events where viscous forces convert some fluid energy into heat. Conversely, in superfluids, which possess zero viscosity, the fluid's total energy remains conserved. It can be contended that due to the inherent simplicity of quantum vortices (zero viscosity, fixed circulation, small core size), quantum vortex reconnections hold significance not only in low-temperature and atomic physics but also contribute to our broader comprehension of fluid phenomena, serving as illustrative models for Euler dynamics.
For more details, see the following related publications.
Guan, H., Zuccher, S. & Liu, X. 2025 Topological cascade of quantum Borromean rings. Physics of Fluids, 37, 024126.
Zuccher, S. & Ricca, R. L. 2022 Creation of quantum knots and links driven by minimal surfaces. Journal of Fluid Mechanics, 942, A8.
Caliari, M. & Zuccher, S. 2021 A fast Time Splitting Finite Difference approach to Gross-Pitaevskii equations. Communications in Computational Physics, 29, 1336-1364.
Zuccher, S. & Caliari, M. 2021 Accurate numerical determination of a self-preserving quantum vortex ring. Journal of Physics A: Mathematical and Theoretical, 54, 015301.
Guan, H., Zuccher, S., Ricca, R. L. & Liu, X. 2020 Topological fluid mechanics and its new developments. (In Chinese, online English translation at this link). Scientia Sinica: Physica, Mechanica et Astronomica, 50, 054701.
Zuccher, S. & Ricca, R. L. 2019 Momentum of vortex tangles by weighted area information. Physical Review E, 100, 011101(R).
Caliari, M. & Zuccher, S. 2018 Reliability of the time splitting Fourier method for singular solutions in quantum fluids. Computer Physics Communications, 222, 46-58.
Zuccher, S. & Ricca, R. L. 2018 Twist effects in quantum vortices and phase defects. Fluid Dynamics Research, 50, 011414.
Zuccher, S. & Ricca, R. L. 2017 Relaxation of twist helicity in the cascade process of linked quantum vortices. Physical Review E, 95, 053109.
Caliari, M. & Zuccher, S. 2017 INFFTM: Fast evaluation of 3d Fourier series in MATLAB with an application to quantum vortex reconnections. Computer Physics Communications, 213, 197-207.
Zuccher, S. & Ricca, R. L. 2015 Helicity conservation under quantum reconnection of vortex rings. Physical Review E, 92, 061001(R).
Allen, A. J. & Zuccher, S. & Caliari, M. & Proukakis, N. P. & Parker, N. G. and Barenghi C. F. 2014 Vortex reconnections in atomic condensates at finite temperature. Physical Review A, 90, 013601.
Zuccher, S., Caliari, M., Baggaley, A. W. & Barenghi, C. F. 2012 Quantum vortex reconnections. Physics of Fluids, 24, 125108.
Caliari, M., Loffredo, M. I., Morato, M. L. & Zuccher, S. 2008 Cubic Nonlinear Schödinger Equation with vorticity. New Journal of Physics, 10, 123020.
TopIn the study of viscous, boundary-layer instability, Tollmien-Schlichting waves are typically considered. The term receptivity is used to define the mechanism through which a generic disturbance present in the external flow or at the wall enters in the boundary layer and produces a wave. The latter can be stable or unstable. When its amplitude exceeds a certain threshold, however, transition from laminar to turbulent motion is observed. On the wing of an aircraft, or on the blades of a turbine, it is convenient to delay this transition so as to reduce the aerodynamic drag and to save in terms of boarded fuel, or to obtain a larger turbine efficiency.
Methods used until today for transition prediction do not consider the effects of disturbances present in the free stream. On the contrary, receptivity calculations have proved that they can be important and should, therefore, be considered. The applications of the receptivity analysis to the aerodynamic design of airplane wings or turbine blades are hence of remarkable interest.
From the theoretical point of view, the problem is solved using perturbation methods such as Multiple Scales. Non parallel effects due to the boundary layer growth are therefore taken into account and the introduction of the non homogeneous version of the multiple scales allows their used for a receptivity approach. The technique, coupled with the solution of the adjoint equations, computed the sensitivity of the solution to the external, exciting disturbances.
Certain coupling behaviors are particularly interesting. Some of them are the interaction between an acoustic wave and the wall roughness, the interaction between a vorticity wave and the wall roughness, the interaction between wall vibration of the wall roughness, and the interaction between a vorticity wave and an acoustic wave, both present in the external flow.
From the result obtained up to now, it is observed that an external perturbation (acoustic or vorticity wave, vibration of the wall, etc.), can induce an unstable wave in the boundary layer only if coupled to a fast adaptation of the boundary layer. This can be achieved, for example, in the zone of the leading edge (as a consequence of the boundary layer growth)or in presence of wall roughness, blowing/suction at the wall, temperature gradient at the wall.
For more details, see the following related publications.
Zuccher, S. & Luchini, P. 2014 Boundary-layer receptivity to external disturbances using multiple scales. Meccanica, 49, 2, 441-467.
Zuccher, S. 2002 Receptivity and control of flow instabilities in a boundary layer, Ph.D thesis, Politecnico di Milano, Milano.
TopIn the case of the Blasius boundary layer it is by now accepted that more than one route to transition is possible. When free-stream disturbances are very small, transition is conceivably preceded by the exponential amplification of Tollmien-Schlichting waves. On the other hand, when somewhat larger perturbations are present, the near-wall region becomes populated by elongated streaks of low and high streamwise velocity.
Early theory was able to explain the presence of the streaks on the basis of a physical argument, named the lift-up effect. Today, most attention has shifted to the fact that the linearized operator governing the amplification of infinitesimal disturbances is highly non-normal and, as a consequence, significant transient amplification of non-modal disturbances can occur even in subcritical flow configurations.
It is reasonable to argue that transition can be spatially delayed if the amplification of the streaks is reduced. A simple way to do that is to employ suction/blowing at the wall to control the growth of the streaks. The term optimal control is here used to denote the best way of controlling a certain initial perturbation. In the context of boundary-layer instabilities, the perturbation kinetic energy is usually taken as an indicator of the level of disturbances, so that the control can be optimized by requiring, for instance, the energy at the end of the flat plate (or the integral of the energy over the streamwise length) to be the lowest.
The simplest approach to identifying the optimal control of a given flow is to impose the worst initial condition and then optimize the control. This procedure is indeed generally known by the name of "optimal control".
Another interesting topic related to flow control is the determination of the linear response of a turbulent system to small-enough perturbations. In view of the flow-control possibilities offered by modern MEMS technology, in fact, the linear-response function can help considerably in controller design, by answering such a basic question as which effects are to be felt here and now if a wall actuator has been moved there and a given time ago. Even though a turbulent flow is a nonlinear phenomenon, a linear response either in the frequency or the time domain can be defined if perturbations are small enough. Using the Direct Numerical Simulation (DNS) tools nowadays available it is possible to describe the complete mean response of a turbulent channel flow to small external disturbances. Space-time impulsive perturbations can be applied at one channel wall, and the linear response describes their mean effect on the flow field as a function of spatial and temporal separations. The turbulent response is shown to differ from the response of a laminar flow with the turbulent mean velocity profile as the base flow.
For more details, see the following related publications.
Luchini, P., Quadrio, M. & Zuccher, S. 2006 The phase-locked mean impulse response of a turbulent channel flow. Physics of Fluids, 18, 121702.
Zuccher, S., Luchini, P. & Bottaro A. 2004 Algebraic Growth of Blasius Boundary Layer: Optimal and Robust Control in the Nonlinear Regime. Journal of Fluid Mechanics 513, 135-160.
Zuccher, S. 2002 Receptivity and control of flow instabilities in a boundary layer, Ph.D thesis, Politecnico di Milano, Milano.
TopClassical hydrodynamic linear stability theory is based on an eigenvalue (normal mode) analysis of the linearized equations of motion, (including the continuity equation) and centers on the characteristics of the fastest growing normal mode. A flow is said unstable if there exists a normal mode with a positive growth rate for the given mean conditions. Nonlinear effects will either instigate a transition of the flow to disorganized turbulence or allow the perturbation to modify the mean flow enough to generate an equilibrium secondary state, which can undergo a further, second instability and successive breakdown to turbulence.
Recently, nonmodal perturbations have been shown to have the potential for large transient energy growth compared to normal modes for a variety of mean flows. The nonmodal stability analysis is based on the fact that for most flows the linear stability equations are not selfadjoint (the eigenfunctions are not orthogonal). We can consider expanding an arbitrary initial perturbation of unit energy using the normalized eigenfunctions as a basis set. Because the basis set is not orthonormal, we will in general have an initial cancellation of contributions between certain combinations of eigenfunctions. However, because the contributions from the different eigenfunctions grow or decay at different rates and have different phase velocities, the initial cancellation of the contributions from nearly parallel eigenfunctions will be removed as space (or time) increases. This could (and typically does) allow transient growth in the energy of the perturbation. Transient growth can occur in subcritical conditions for which no eigenvalue has a positive growth rate. In supercritical conditions, this transient growth can greatly exceed the exponential growth of the unstable normal mode over a finite time interval.
Optimal perturbations provide an upper bound for this energy growth, as they are defined as the the initial conditions for the boundary layer equautions, that cause the highest energy growth (from which the term "optimal"). These initial conditions are optimal in the sense that at the end of any chosen space (or time) domain, no other perturbation will achieve a larger increase in energy density.
For more details, see the following related publications.
Zuccher, S., Tumin, A. & Reshotko, E. 2006 Parabolic Approach to Optimal Perturbations in Compressible Boundary Layers. Journal of Fluid Mechanics, 556, 189-216.
Zuccher, S., Shalaev, I., Tumin, A. & Reshotko, E. 2006 Optimal Disturbances in the Supersonic Boundary Layer Past a Sharp Cone. AIAA Paper 2006-1113.
Zuccher, S., Tumin, A. & Reshotko, E. 2005 Optimal Disturbances in Compressible Boundary Layers - Complete Energy Norm Analysis. AIAA Paper 2005-5314.
Zuccher, S., Luchini, P. & Bottaro A. 2004 Algebraic Growth of Blasius Boundary Layer: Optimal and Robust Control in the Nonlinear Regime. Journal of Fluid Mechanics 513, 135-160.
Zuccher, S., Bottaro A., & Luchini, P. 2006 Algebraic growth in a Blasius boundary layer: Nonlinear optimal disturbances. European Journal of Mechanics B 25, 1-17.
Zuccher, S. & Luchini, P. 2002 Time-Dependent Optimal Perturbations for the Algebraic Instability in the Nonlinear Regime. In Proceedings of the 2002 ASME Fluids Engineering Division Summer Meeting, American Society of Mechanical Engineers, Fluids Engineering Division FED, Volume 257, Issue 1 B, 2002, Pages 1387-1393. Montreal, Quebec, Canada.
Zuccher, S. 2002 Receptivity and control of flow instabilities in a boundary layer, Ph.D thesis, Politecnico di Milano, Milano.
TopThe interest in swept wings for high-speed applications is due to the fact that in supersonic regimes a bow shock-wave originates in front of "regular" wings, i.e. straight wings with rounded-nose airfoil, leading to an area of very high pressure just ahead of the leading edge. This dramatically increases the drag and hence the fuel consumption. If the wing is swept backwards, however, the pressure drop across the shock wave is reduced and so is the wave drag. When the sweep is large enough so that the leading edge is completely contained within the so-called Mach angle, the flow in front of the leading edge itself is subsonic and the shock wave cannot originate. This eliminates completely the wave drag. Besides wave-drag reduction/elimination, other advantages of swept wings are the reduction of sonic-boom effects in supersonic flight and the increase of critical Mach number in transonic flight.
If wave drag can be reduced or totally eliminated by sweeping the wing, a more difficult-to-control source of drag is skin-friction due to viscous effects, which take place inside the boundary layer. This type of drag is directly related to laminar-to-turbulent boundary-layer transition, which in high Mach-number regimes affects not only drag but also heat loads because of mixing enhancement, typical of turbulent flows. Allowing laminar flow over most of the wing of a modern airplane, therefore, would result in remarkable engineering benefits. This is the reason why transition to turbulence in boundary layers has received a considerable attention over the past decades.
From the point of view of practical applications, the understanding of basic transition mechanisms will allow us to employ flow control strategies in order to delay or avoid turbulence. Among these, passive ones would probably be preferable since they are more easily realizable and, in general, require less complications and less maintenance compared to active flow strategies.
Despite considerable efforts, the physics of transition in high-speed boundary layers are still poorly understood, in part due to the lack of experiments. By presenting some results in supersonic swept-wing flows, the present study aims at proposing infrared thermography as a technique to easier this type of investigations.
Thanks to the state-of-the-art infrared equipment available today, greater success and improved resolution of details of various flow phenomena have become possible in the last years. Since modern infrared cameras are able to measure temperature difference with an accuracy of nearly a tenth of a degree over a small area, infrared thermography (IRT) represents a very powerful tool to visualize flow phenomena that create measurable temperature changes on the model, such as shock waves, flow separation and laminar-to-turbulent boundary-layer transition.
The basic principle behind the use of IRT for transition-detection is the difference in the convective heat-transfer coefficients between laminar and turbulent flows. The laminar boundary layer allows very low heat exchanges between the model surface and the surrounding freestream flow. Laminar regions are thus characterized by a very low convective heat-transfer coefficient and behave as an insulator when compared with turbulent regions. In practice, this means that the surface in presence of laminar flow has the tendency to keep its initial temperature, which, in general, is different from the temperature of the external flow. On the contrary, the turbulent boundary layer features high mixing and therefore high convective heat exchange. As a direct consequence, a surface characterized by a turbulent boundary layer will reach the temperature of the surrounding, incoming flow faster than a laminar boundary layer.
IRT can offer several advantages compared to the other quantitative techniques previously presented. The set-up and the necessary acquisition system is very simple and compact. There is no need to paint or spray polymers, liquids or other substances on the model surface before each run and external light sources (like UV or others) are not necessary. Moreover, the user is not required to perform any calibration, being done and certified directly by the vendor. Like TSP, IRT can be used as a quantitative measurement technique or qualitative flow visualization tool. It provides a global flow-field image without the necessity of multiple local measurements (contrary to thermocouples) and if local information is needed, data can be retrieved from the whole image using the post-processing software that comes with the most common IR cameras used for scientific purposes. Besides all these advantages, IRT is perhaps the least intrusive technique because it does not require any kind of modification or interaction with the model or the flow, which could alter the phenomenon under investigation. This is preferable when transition is studied because of its extreme sensitivity to environmental disturbances via receptivity. In some cases, if a better image contrast is needed, the model can be heated or cooled with respect to its natural temperature, making IRT more intrusive. In general, however, IRT is a very poorly intrusive technique.
For more details, see the following related publications.
Zuccher, S. & Saric, W. 2008 Infrared Thermography Investigations in Transitional Supersonic Boundary Layers. Experiments in Fluids, 44, 1, 145-157.
Zuccher, S., Saric, W., Reed H. & McNeil, L. 2003 The Role of Infrared Thermography in the Study of Crossflow Instability at M=2.4. In Proceedings of the 7th Triennial International Symposium on Fluid Control, Measurement and Visualization. Sorrento, Italy.
TopFormation of superficial waves is observed during the wire coating process, which aims at covering a small-radius cylinder with a thin layer of another material, initially liquid, so as to protect or paint textile fibers, optical fibers, electric wires, etc. The presence of these waves can have consequences on aesthetic finish or on the characteristics of the product (i.e. thermal exchange coefficient because the surface increases).
In order to understand the way in which these instabilities occur, experimental tests are carried out measuring the thickness of the liquid that covers the wire before its drying, and deducing amplitude and characteristic wavelength of the superficial wave. This measurements are obtained through a new technique based on laser plane probes. The use of two equal probes allows the experimental measurement of the wave velocity and the amplification (or damping) factor from the same wave.
In the case of simple withdrawal of the wire from the liquid bath, or when an orifice is used for controlling the final thickness (die coating ), the obtained results agree with the existing theories found in literature. If an annular jet is used to control the final thickness of the coating (annular jet wiping), no existing theories can be applied for comparison. A new model is therefore developed, which reveals very good agreement with experimental data. For certain ranges of the dragging wire velocity and for certain values of jet pressure, the formation of waves is observed, while in other cases this can be controlled or even eliminated.
For more details, see the following related publications.
Zuccher, S. 2009 An experimental study of the liquid film on a vertical wire under the action of an impinging annular jet. Experiments in Fluids, 46, 2, 309-322.
Zuccher, S. 2005 A novel measurement technique for the study of wire coating instabilities. Experiments in Fluids 39, 4, 694-702.
Zuccher, S. & Buchlin, J.-M. 2001 Liquid film instabilities in die coating process. In Advances in Coating Processes. Proceedings of 4th European Coating Symposium 2001, Free University of Brussels, Belgium.
Buchlin, J.-M. & Zuccher, S. 1999 Liquid film instability of wire coating. In Advances in Coating and Drying of Thin Films. Proceedings of 3rd European Coating Symposium 1999. University of Erlangen-Nürnberg, Germany.
Zuccher, S. 1999 Liquid film instabilities of wire coatings, von Karman Institute for Fluid Dynamics, Rhode-Saint-Genèse, Bruxelles.
TopCan the spin of an airplane be considered a chaotic motion? The origin of such a doubt resides in the fact that in certain cases the spin motion turns out to be very complex (the so-called anomalous spin) and the recovery of the aircraft is very difficult or even not possible. Moreover, since it happens at angles of attack for which nonlinear effects are important, the spin could introduce chaotic aspects.
In order to find an answer, wind tunnel tests are carried out on a model of a fighter aircraft attached to its center of gravity through an universal joint that allows only the three rotations. The angles that define the three degrees of freedom are analyzed using the typical tools of the theory of the chaos, such as power spectra, projections of the attractor in the phase space, reconstruction in the embedding space and Poincare sections.
From the analysis of the data, it can be deduced that increasing the wind tunnel velocity, i.e. the Reynolds number, successive bifurcations in the frequencies of the motion, a more complex structure of the attractor with fractal aspects and sensitivity to initial conditions are found. These hints could make one think about an evolution towards chaos, however true chaotic motion is not fully observed.
Other configurations are also analyzed, by changing the nose of the model or the wings, so as to verify the influence of these particulars on the motion. The conclusion is that, for certain configurations, a development of the motion towards chaos is observed; for others the motion turns out be very regular. Visualizations with smoke confirm the hypotheses concerning the aerodynamic interaction between the wings and the vortices produced from the nose and between the tail-planes and the wake due to the wings.
For more details, see the following related publications.
Zuccher, S. & De Ponte, S. 2007 Post-Stall Motions Evolving Toward Chaos. Journal of Aircraft, 44, No. 3, 833-844.
Zuccher, S. 1997 Moti Caotici Post-Stallo, Master Thesis, Politecnico di Milano, Milano.
Top